• Drucken

Dynamische Fehlerkompensierung

Die vorgegebene Sollposition (x_s0 ,y_s0) auf einem realen Kreuztisch wird nicht erreicht, weil der Aufbau eines solchen mit Verfahrachsen in X- und Y-Richtung nicht ideal ist. Der reale Kreuztisch weicht vom seinem idealen Pendant, betrachtet man nur die 2D-Ebene, in zwei Punkten ab:

1. Existenz von Längenfehlern (δX, δY): Ursache hierfür sind z. B. ein fehlendes Messsystem direkt am interessierenden Punkt [xs0 ,ys0] (z. B. der Laserstrahl auf dem Werkstück), was z. B. bei Spindelachsen ohne zusätzlich lastseitig montiertes Messsystem der Fall ist (durch Spindelsteigungsfehler, Umkehrspiel, Lose). Auch Direktantriebe (z. B. Linearantriebe), die prinzipbedingt diese Ursachen ausschließen und den Lageregler mit Messwerten direkt vom interessierenden Punkt schließen, haben durch Fertigungs- und Montagefehler des Maßstabs selbst eine systematische Fehlerquelle.
2. Winkelfehler (φX, φY): Bewegungen einer „senkrechten“ Achse auf der eigenen Koordinate haben nur dann keinen Einfluss auf die korrekte Position der jeweils andere Achse, wenn die Montage der Achsen ideal orthogonal (φX, φY = 0) ist, was bei realen Achsen nicht der Fall ist. Zu beachten ist, dass sowohl in X- als auch Y-Richtung Winkelfehler auftreten. Das Ausrichten des Kreuztisches entlang einer idealen Achse XS bzw. YS ist nicht in jedem Fall möglich oder gewünscht.

Stand der Technik

Für das Einmessen (Bestimmung der Abweichungen) der 1D-Längenfehlers muss man während des Messens und nachfolgenden Prüfens die 2D-Winkelfehlerkorrektur ausschalten, da beim zeitaufwendigen Einmessen, z. B. mittels Laserinterferometern, durch Dienstleister oft nur 1D-Längenfehler des Messsystems bzw. bei Linearachsen mit Spindel der Spindelsteigungsfehler mit vertretbarem Aufwand gemessen werden können. Häufig liefern Hersteller komplett montierte Linearachse mit Messprotokoll, wobei sich die Längenfehler auf den Index des Messsystems beziehen.

 Kombinierte 1D-/2D-Korrektur mit ACS Motion Control

Wenn man zum Winkelfehler den Längenfehler kompensieren will, ist der Wert (x_S, y_S) für die Berechnung durch ( (x_S + δ_X), ( y_S + δ_Y)) zu ersetzen, da auch die Längenkorrektur selbst wegen des Winkelfehlers korrigiert werden muss. Der Korrektur-Ansatz bei ACS Motion Control¹ basiert auf einem Array-Ansatz, bei dem aktuelle Korrekturwerte für X und Y getrennt aus einem 2D-Array mit den Indizes x_S und y_S (interpolierte Werte, da das Array in Zeilen- und Spaltenanzahl endlich ist) ausgelesen und auf die aktuellen Positionssollwerte x_S und y_S addiert werden. Für X und Y werden diese Operationen getrennt ausgeführt. Ein wesentlicher Grund, Positionswerte über 2D-Arrays zu korrigieren, ist vor allem ein technischer. Ein ptp-Befehl (Point-to-Point) zum Positionieren von Achsen bezieht sich auf den Endpunkt der Positionierung (relativ zur aktuellen Sollposition oder absolut, jeweils im Vektorraum S). Will man auch die Trajektorie (die Positionsfolge zur Zielposition) korrigieren, müsste man jeden einzelnen Bewegungspunkt (auf einer Zeitachse) berechnen und zeitsynchron an jede beteiligte Achse übermitteln, was technisch aufwendig ist und vor allem von Standard-Befehlsgebung (PLCopen z. B. „MC_MoveAbsolute“, ACS „ptp“) abweicht.

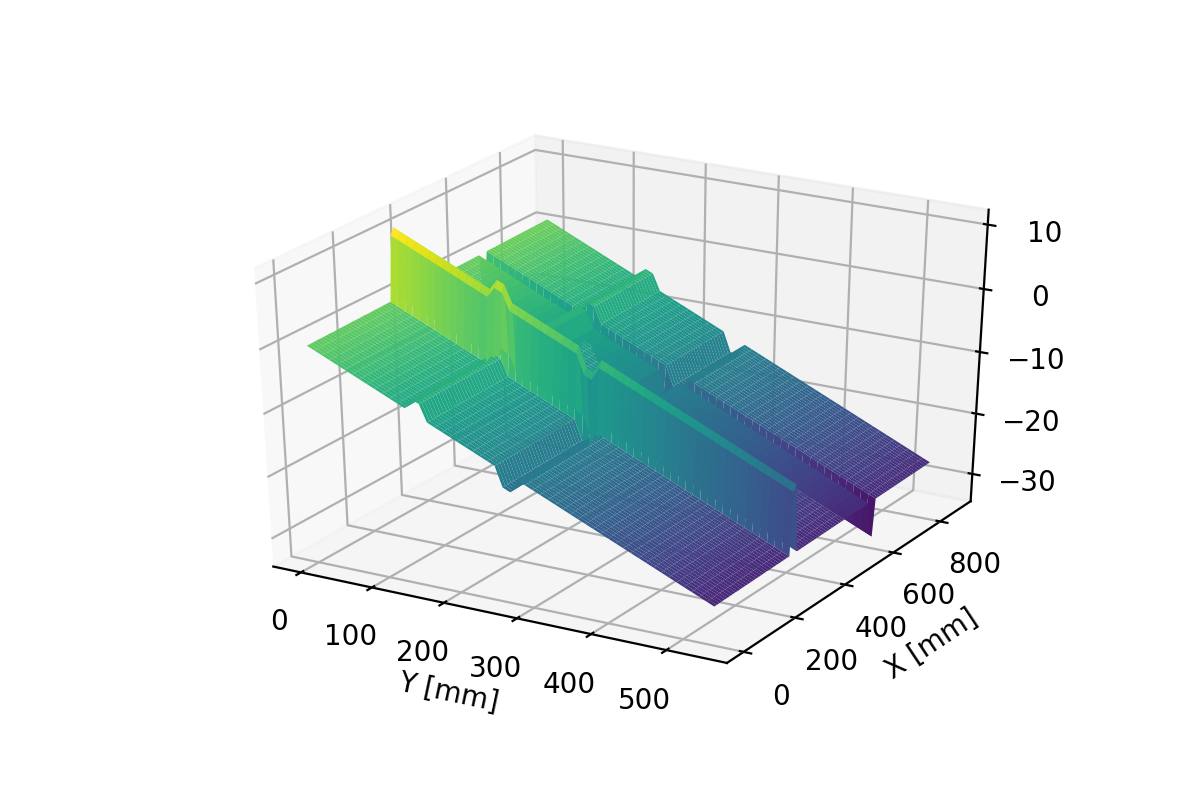
Das folgende Bild zeigt die kombinierte Fehlerkorrektur von Längen- und Winkelfehlern mittels 2D-Sollwertgenerierung. Die Kalkulation der Korrekturen erfolgt über eine sogenannte Change-of-Base-Berechnung. Die Berechnungen können online im ACS-Controller als auch mittels externem Python-Programm erfolgen. Im Beispiel sind die Korrekturdiagramme für Längenfehler und kombinuerte Längen-/Winkelfehler in der X-Achse als Funktion von Achspositionen X und Y und Längenfehlern der X-Achse dargestellt.